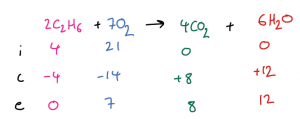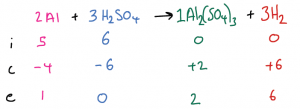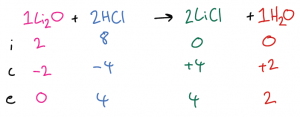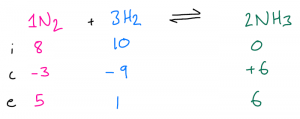A balanced symbol equation tells us the ratio between the changes in the number of moles of each substance in a reaction.
If: 2 C2H6 + 7 O2 –> 4 CO2 + 6 H2O
Then: the moles of C2H6, O2, CO2 and H2O change in a 2:7:4:6 ratio.
A very common type of question in Chemistry is where we need to calculate the amount of each product formed from an initial amount of reactants. One of the most efficient ways to do this this calculation is to use an ICE table (Initial – Change – End).
The most basic type of ICE table will have four rows. The top row will be the balanced symbol equation. The other rows show the initial (I), change (C) and end (E) number of moles for each substance.
The basic process is:
- Write out the balanced symbol equation
- Fill in the initial moles of all reactants and products. The initial moles of the products will be zero.
- Fill in the change and end moles for one of the substances.
- Use the ratios in the balanced symbol equation to fill in the change moles for the rest of the substances. This will be negative for reactants and positive for products.
- Use the initial and change moles to fill in the end moles for the rest of the substances
Here’s a specific example of how to use an ICE table for the reaction above:
| Example 1: 4 mol of C2H6 are mixed and react with 21 mol of O2. Calculate the amount of CO2 and H2O produced. First, we write out the balanced symbol equation at the top of the ICE table, and fill in the initial moles for both reactants and also both products. The next step is probably the hardest. We can assume that the reaction goes to completion so we need to determine the limiting reactant. There is a process you can follow: simply divide each of the initial moles of reactant by the number in front of it in the balanced symbol equation, then compare your results, i.e., for C2H6: 4 / 2 = 2 and for O2: 21 / 7 = 3. The substance which gives the smallest result (i.e., C2H6) is the limiting reagent. Since it is used up completely in the reaction, its end amount will be zero and its change amount will be -4. The balanced symbol equation tells us that the moles of C2H6, O2, CO2 and H2O change in a 2:7:4:6 ratio. By applying this ratio to the changes, we can work out the change for all other substances in the reaction. Finally, use the initial and change amounts to calculate the end amounts for the other substances. |
Here is another example:
| Example 2: 5 mol of Al are mixed with 6 mol of H2SO4 and react. Calculate the amount of Al2(SO4)3 and H2 produced. First, we write out the balanced symbol equation at the top of the ICE table, and fill in the initial moles for both reactants and also both products. Then, determine which is the limiting reactant. i.e., Al: 5 / 2 = 2.5 and H2SO4: 6 / 3 = 2. The result for H2SO4 is smaller so it is the limiting reactant. The end amount of H2SO4 is therefore 0 and the change is -6. Then, use the 2:3:1:3 ratio in the balanced symbol equation to complete the change row for the other substances Finally, use the initial and change amounts to calculate the end amounts for the other substances.
|
And another example:
| Example 3: 2 mol Li2O are mixed and react with 8 mol HCl. Calculate the amount of LiCl and H2O produced. First, write out the balanced symbol equation at the top of the ICE table, then fill in the initial moles of all substances. Then, decide which is the limiting reactant (in this case, it is Li2O) and complete the end and change amounts for the limiting reactant. Then, use the ratio in the balanced symbol equation to complete the change row for all the other substances Finally, use the initial and change amounts to calculate the end amounts for all the other substances.
|
The three reactions we have looked at so far all go to completion. This means that at least one of the reactants is used up completely, so it ends with zero moles. However, ICE tables can also be used for reversible reactions:
| Example 4: 8 mol N2 are mixed and react with 10 mol H2. The amount of H2 present in the final mixture is 1 mol. Calculate the moles of N2 and NH3 present. First, write out the balanced symbol equation at the top of the ICE table, then fill in the initial moles of all substances. Then, we are told the end amount of H2, so we can work out the change amount. In this case, there is no limiting reactant so the calculation is even more straightforward! Then, use the ratio in the balanced symbol equation to complete the change row for all the other substances Finally, use the initial and change amounts to calculate the end amounts for all the other substances.
With a few more steps, this approach would then allow us to calculate the equilibrium constants Kc and Kp. |
In summary: you will find ICE tables useful whenever there is a limiting reactant to consider or the reaction is reversible.
Next, in Big Idea #4, we’ll look at how to balance redox equations. This is the next step on the way to being able to tackle the most challenging titrations on the A Level Chemistry course.